В первую очередь, необходимо на достаточном для понимания сути уровне разобраться в том, как строить саму изометрию – то есть метрическое плоское пространство. Начинать нужно с самых основ, связанных с работой с изометрическими проекциями и плоскостями. Они включают в себя построение простейших и обычных плоских линий, лишь после освоения которых можно переходить к изучению форм. Вполне естественно, что без знания азов ни у кого не выйдет перескочить сразу к различным цилиндрическим формам, ведь проблема возникнет сразу же на этапе построения таких более сложных по сравнению с линиями фигур, как квадрат, а затем и круг в изометрии. Многие выдвигают такую точку зрения, что именно окружность является одной из наиболее проблематичных для изображения в проекции среди всех плоских фигур.
Изображение изометрической проекции
Сама суть проекции состоит в том, что какой-либо существующий трехмерный объект или фигура отображается на изометрической плоскости, при этом сохраняется отношение длины спроектированных отрезков к действительной длине. Другими словами, коэффициент искажения остается неизменным по всем трем осям. Этим и отличается изометрическая проекция, так как только при ней все имеющиеся масштабы остаются одинаковыми.
Изометрическая проекция возможна при соблюдении условия, чтобы углы между осями проекции были одинаковыми и равны 120 градусам. У подобной проекции есть достоинство, благодаря чему ее так часто используют в различных чертежах и проектах. Причина кроется в том, что при изменении расстояния сами отражаемые объекты при этом не кажутся меньше или больше, чем они есть на самом деле.
Однако у изометрических проекций существуют и свои недостатки. Так, например, если на рисунке отсутствуют обозначающие тени на разных сторонах, то будет крайне сложно определить, какая из сторон фигуры на данный момент находится к нам ближе и, собственно, наблюдается. Кроме того, будет проблематично понять, где у объекта располагаются верхняя и нижняя грань, из-за наличия двух крайне схожих проекций, равных по площади и размерам.
Смотрите видео об окружности в изометрии.
Как чертить круг в изометрии?
Все, кто на каком-либо из этапов обучения сталкиваются с вопросом, как начертить круг в изометрии, очень часто совершают типичные и распространенные среди новичков ошибки.
Основные факторы при построении изометрической проекции, которые нужно запомнить, заключаются в нескольких деталях:
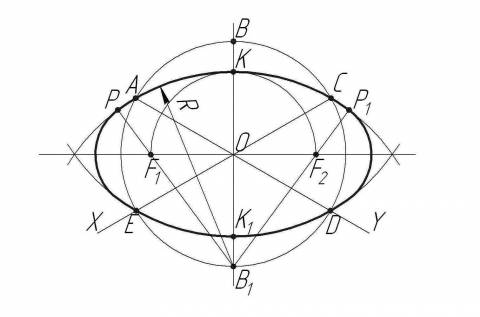
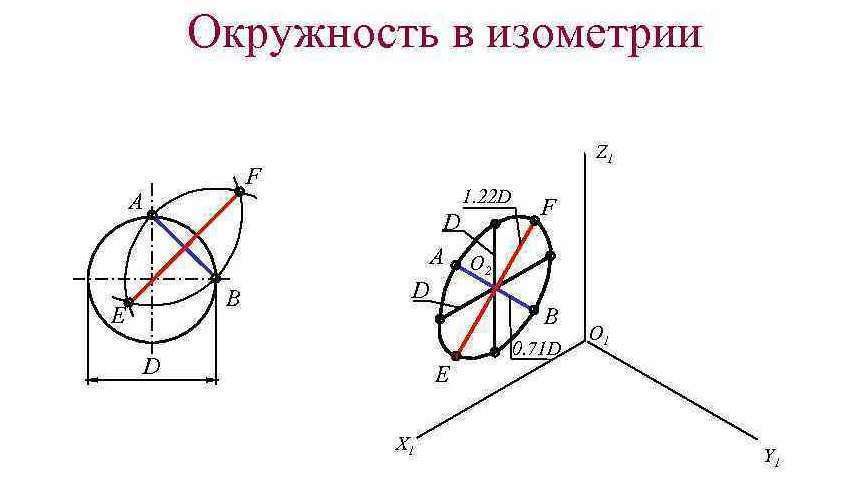
- Дело в том, что в случаях вычерчивания в изометрии окружность изображается не в своем первоначальном положении. В конечном итоге она должна принять форму эллипса.
- Вдобавок к этому, есть важный элемент, который задает курс всему последующему построению. Нужно ориентироваться на тот момент, что любую окружность можно рассматривать как правильный многоугольник, в котором может быть неограниченное множество сторон.
Как уже было сказано, в изометрическом пространстве окружность отображается в виде эллипса. Но начинающие регулярно сталкиваются с проблемами, так как он достаточно сложен для построения. В связи с данным фактом часто рекомендуется прибегать к использованию овалов как оптимальной замене эллипсам.
Всего существует несколько инструкций для разных способов, как чертить круг в изометрии через овал. В нашем же случае будет рассмотрен один из наиболее часто используемых и распространенных. Первоочередным этапом является вычисление размеров самих осей фигуры, большой и малой, по формулам через диаметр окружности, изометрическую проекцию которой необходимо вычертить.
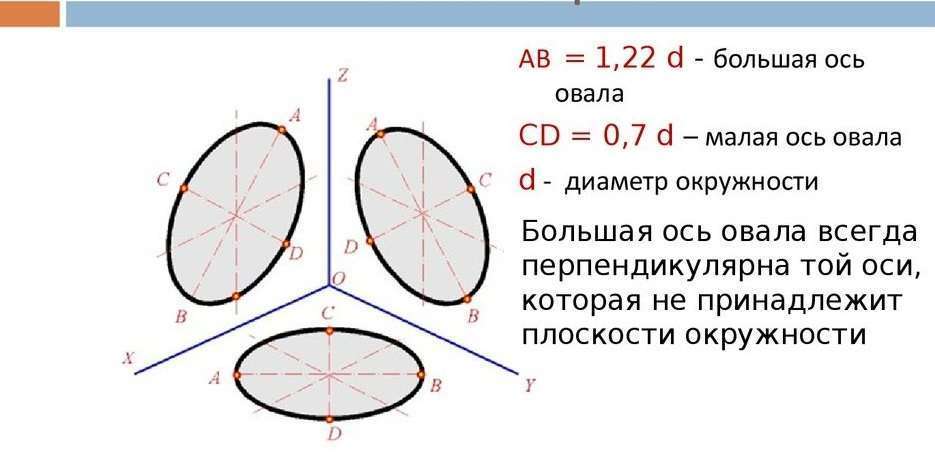
Существует также и графический способ определения осей эллипса, который изучается наглядным путем. Для вычисления малой оси требуется соединить между собой ближайшие точки перпендикулярных прямых линий, проведенных через центр окружности, лежащие на этой самой окружности. Дальше через эти точки проводятся дуги радиусов так, чтобы они пересеклись между собой. Данные точки пересечения будут образовывать линию, которая, в свою очередь, является большой осью.
Читайте о том, как найти площать правильного и неправильного шестиугольника.
А также о технике устного счета.
Круг в изометрии: построение
Руководство, как нарисовать круг в изометрии, не заканчивается на вычислении размеров осей. В зависимости от принадлежности к какой-либо из координатных плоскостей, устанавливается направление вычисленных и построенных ранее осей овала. Следом за этим по размерам обеих осей проводятся окружности. При их пересечении выделяются четыре точки, которые впоследствии послужат центрами дуг необходимого нам овала.
Так как приводимая поэтапная инструкция приводится скорее для новичков, которые только учатся, как сделать круг в изометрии, то следует подробнее рассмотреть процесс определения направления осей вычерчиваемого эллипса. Прежде всего, это зависит непосредственно от положения самой окружности, которую требуется спроецировать.
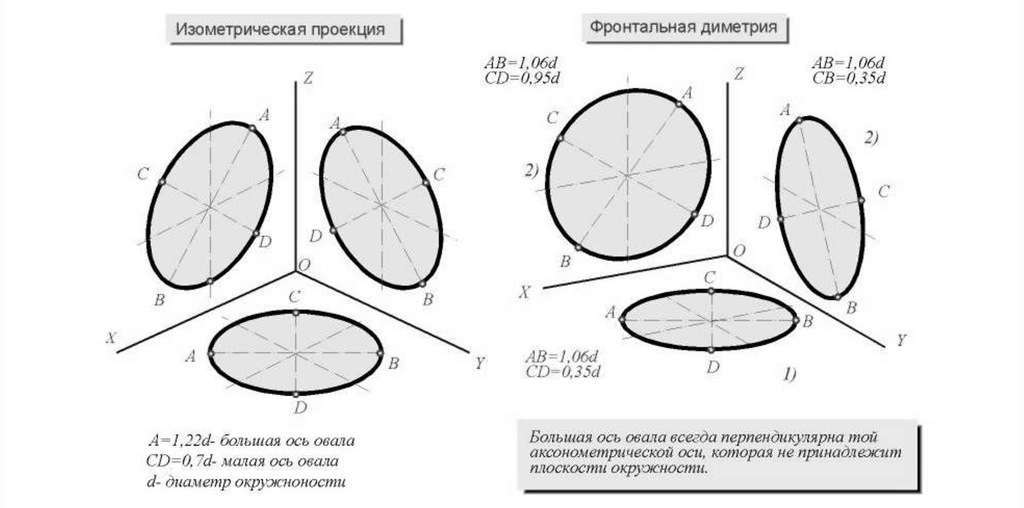
При построении всегда соблюдается одно негласное правило: при любых обстоятельствах большая ось будет расположена перпендикулярно к оси, которая проецируется в точку на данной плоскости. Малая ось при этом обязательно совпадает по направлению с этой осью.
Чтобы впоследствии, после завершения всех расчетов и непосредственного построения проекции, у других людей, не знакомых изначально с вашим чертежом, не возникали трудности с определением сторон, используется нанесение теней и штриховки. При этом очень важным условием является направление имеющихся штрихов. Так, например, принято, что в изометрической проекции линии должны совпадать по своей направленности либо с большими диагоналями квадрата, в который вписана окружность, либо с малыми.
Помимо этого, чтобы в дальнейшем упростить задачу людям, которым предстоит работать по данным чертежам, зачастую на рисунок наносятся еще и тени, отбрасываемые вычерченной проекцией. Это не только сводит к минимуму возникновение недопонимания, но и делает проект в эстетическом плане более приятным для восприятия.
Остались ли у вас вопросы по теме? Задайте их в комментариях! А также смотрите видео о построении изометрии окружности.